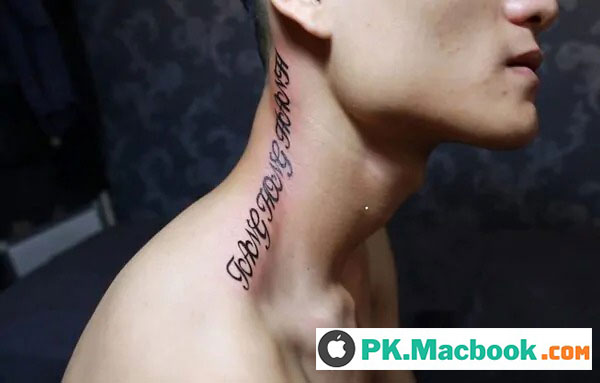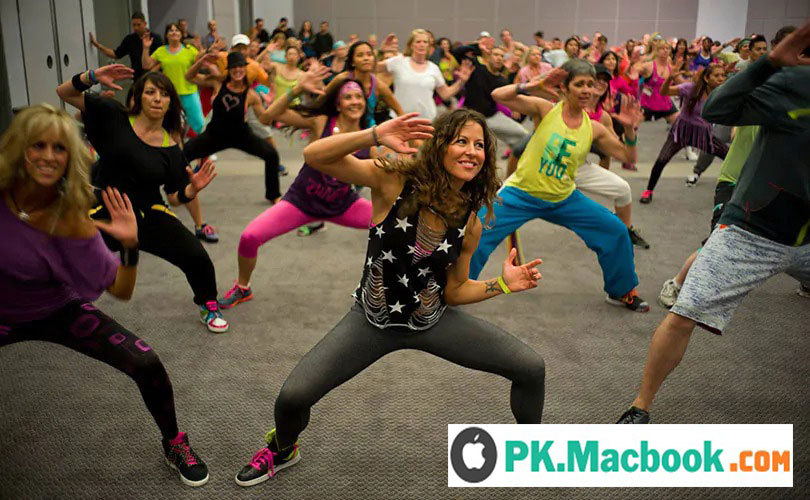Bạn đang xem: Tổng hợp các phương pháp phân tích đa thức thành nhân tử (cơ bản & nâng cao)

Bạn đang xem: Tổng hợp các phương pháp phân tích đa thức thành nhân tử (cơ bản & nâng cao) Tại Pkmacbook.com

9C vô đối ! :: Góc học tập :: KH tự nhiên Share |

Mục lục hiện

Tổng hợp các phương pháp phân tích đa thức thành nhân tử (cơ bản & nâng cao)

Xem chủ đề cũ hơn Xem chủ đề mới hơn Go down Tác giảThông điệp

Chau Linh – Admin

Posts

176

Points

330

Thanked

Join date

09/05/2011

Age

Đến từ

Thanh Hóa

Admin17633009/05/201124Thanh Hóa

Bài gửi Tiêu đề: Tổng hợp các phương pháp phân tích đa thức thành nhân tử (cơ bản & nâng cao) Fri Jun 24, 2011 1:43 pm

Tiêu đề: Tổng hợp các phương pháp phân tích đa thức thành nhân tử (cơ bản & nâng cao)Fri Jun 24, 2011 1:43 pm

I. CÁC PHƯƠNG PHÁP CƠ BẢN

1. Phương pháp đặt nhân tử chung

– Tìm nhân tử chung là những đơn, đa thức có mặt trong tất cả các hạng tử.

– Phân tích mỗi hạng tử thành tích của nhân tử chung và một nhân tử khác.

– Viết nhân tử chung ra ngoài dấu ngoặc, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng).

Ví dụ 1. Phân tích các đa thức sau thành nhân tử.

28a2b2 – 21ab2 14a2b = 7ab(4ab – 3b 2a)

2x(y – z) 5y(z –y ) = 2(y – z) – 5y(y – z) = (y – z)(2 – 5y)

xm xm 3 = xm (x3 1) = xm( x 1)(x2 – x 1)

2. Phương pháp dùng hằng đẳng thức

– Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.

– Cần chú ý đến việc vận dụng hằng đẳng thức.

Ví dụ 2. Phân tích các đa thức sau thành nhân tử.

9×2 – 4 = (3x)2 – 22 = ( 3x– 2)(3x 2)

8 – 27a3b6 = 23 – (3ab2)3 = (2 – 3ab2)( 4 6ab2 9a2b4)

25×4 – 10x2y y2 = (5×2 – y)2

3. Phương pháp nhóm nhiều hạng tử

– Kết hợp các hạng tử thích hợp thành từng nhóm.

– Áp dụng liên tiếp các phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức.

Ví dụ 3. Phân tích các đa thức sau thành nhân tử

2×3 – 3×2 2x – 3 = ( 2×3 2x) – (3×2 3) = 2x(x2 1) – 3( x2 1)

= ( x2 1)( 2x – 3)

x2 – 2xy y2 – 16 = (x – y)2 – 42 = ( x – y – 4)( x –y 4)

4. Phối hợp nhiều phương pháp

– Chọn các phương pháp theo thứ tự ưu tiên.

– Đặt nhân tử chung.

– Dùng hằng đẳng thức.

– Nhóm nhiều hạng tử.

Ví dụ 4. Phân tích các đa thức sau thành nhân tử

3xy2 – 12xy 12x = 3x(y2 – 4y 4) = 3x(y – 2)2

3x3y – 6x2y – 3xy3 – 6axy2 – 3a2xy 3xy =

= 3xy(x2 – 2y – y2 – 2ay – a2 1)

= 3xy[( x2 – 2x 1) – (y2 2ay a2)]

= 3xy[(x – 1)2 – (y a)2]

= 3xy[(x – 1) – (y a)][(x – 1) (y a)]

= 3xy( x –1 – y – a)(x – 1 y a)

II. PHƯƠNG PHÁP TÁCH MỘT HẠNG TỬ THÀNH NHIỀU HẠNG TỬ

1. Đối với đa thức bậc hai (f(x) = ax2 bx c)

a) Cách 1 (tách hạng tử bậc nhất bx):

Bước 1: Tìm tích ac, rồi phân tích ac ra tích của hai thừa số nguyên bằng mọi cách.

a.c = a1.c1 = a2.c2 = a3.c3 = … = ai.ci = …

Bước 2: Chọn hai thừa số có tổng bằng b, chẳng hạn chọn tích a.c = ai.ci với b = ai ci

Bước 3: Tách bx = aix cix. Từ đó nhóm hai số hạng thích hợp để phân tích tiếp.

Ví dụ 5. Phân tích đa thức f(x) = 3×2 8x 4 thành nhân tử.

Hướng dẫn

– Phân tích ac = 12 = 3.4 = (–3).(–4) = 2.6 = (–2).(–6) = 1.12 = (–1).(–12)

– Tích của hai thừa số có tổng bằng b = 8 là tích a.c = 2.6 (a.c = ai.ci).

– Tách 8x = 2x 6x (bx = aix cix)

Lời giải

3×2 8x 4 = 3×2 2x 6x 4 = (3×2 2x) (6x 4)= x(3x 2) 2(3x 2)

= (x 2)(3x 2)

b) Cách 2 (tách hạng tử bậc hai ax2)

– Làm xuất hiện hiệu hai bình phương :

f(x) = (4×2 8x 4) – x2 = (2x 2)2 – x2 = (2x 2 – x)(2x 2 x)

= (x 2)(3x 2)

– Tách thành 4 số hạng rồi nhóm :

f(x) = 4×2 – x2 8x 4 = (4×2 8x) – ( x2 – 4) = 4x(x 2) – (x – 2)(x 2)

= (x 2)(3x 2)

f(x) = (12×2 8x) – (9×2 – 4) = … = (x 2)(3x 2)

c) Cách 3 (tách hạng tử tự do c)

– Tách thành 4 số hạng rồi nhóm thành hai nhóm:

f(x) = 3×2 8x 16 – 12 = (3×2 – 12) (8x 16) = … = (x 2)(3x 2)

d) Cách 4 (tách 2 số hạng, 3 số hạng)

f(x) = (3×2 12x 12) – (4x Cool = 3(x 2)2 – 4(x 2) = (x 2)(3x – 2)

f(x) = (x2 4x 4) (2×2 4x) = … = (x 2)(3x 2)

e) Cách 5 (nhẩm nghiệm): Xem phần III.

Chú ý : Nếu f(x) = ax2 bx c có dạng A2 ± 2AB c thì ta tách như sau :

f(x) = A2 ± 2AB B2 – B2 c = (A ± B)2 – (B2 – c)

Ví dụ 6. Phân tích đa thức f(x) = 4×2 – 4x – 3 thành nhân tử.

Hướng dẫn

Ta thấy 4×2 – 4x = (2x)2 – 2.2x. Từ đó ta cần thêm và bớt 12 = 1 để xuất hiện hằng đẳng thức.

Lời giải

f(x) = (4×2 – 4x 1) – 4 = (2x – 1)2 – 22 = (2x – 3)(2x 1)

Ví dụ 7. Phân tích đa thức f(x) = 9×2 12x – 5 thành nhân tử.

Lời giải

Cách 1 : f(x) = 9×2 – 3x 15x – 5 = (9×2 – 3x) (15x – 5) = 3x(3x –1) 5(3x – 1)

= (3x – 1)(3x 5)

Cách 2 : f(x) = (9×2 12x 4) – 9 = (3x 2)2 – 32 = (3x – 1)(3x 5)

2. Đối với đa thức bậc từ 3 trở lên (Xem mục III. Phương pháp nhẩm nghiệm)

3. Đối với đa thức nhiều biến

Ví dụ 11. Phân tích các đa thức sau thành nhân tử

a) 2×2 – 5xy 2y2 ;

b) x2(y – z) y2(z – x) z2(x – y).

Hướng dẫn

a) Phân tích đa thức này tương tự như phân tích đa thức f(x) = ax2 bx c.

Ta tách hạng tử thứ 2 :

2×2 – 5xy 2y2 = (2×2 – 4xy) – (xy – 2y2) = 2x(x – 2y) – y(x – 2y)

= (x – 2y)(2x – y)

a) Nhận xét z – x = -(y – z) – (x – y). Vì vậy ta tách hạng tử thứ hai của đa thức :

x2(y – z) y2(z – x) z2(x – y) = x2(y – z) – y2(y – z) – y2(x – y) z2(x – y) =

= (y – z)(x2 – y2) – (x – y)(y2 – z2) = (y – z)(x – y)(x y) – (x – y)(y – z)(y z)

= (x – y)(y – z)(x – z)

Chú ý :

1) Ở câu b) ta có thể tách y – z = – (x – y) – (z – x) (hoặc z – x= – (y – z) – (x – y))

2) Đa thức ở câu b) là một trong những đa thức có dạng đa thức đặc biệt. Khi ta thay x = y (y = z hoặc z = x) vào đa thức thì giá trị của đa thức bằng 0. Vì vậy, ngoài cách phân tích bằng cách tách như trên, ta còn cách phân tích bằng cách xét giá trị riêng (Xem phần VII).

III. PHƯƠNG PHÁP NHẨM NGHIỆM

Trước hết, ta chú ý đến một định lí quan trọng sau :

Định lí : Nếu f(x) có nghiệm x = a thì f(a) = 0. Khi đó, f(x) có một nhân tử là x – a và f(x) có thể viết dưới dạng f(x) = (x – a).q(x)

Lúc đó tách các số hạng của f(x) thành các nhóm, mỗi nhóm đều chứa nhân tử là x – a. Cũng cần lưu ý rằng, nghiệm nguyên của đa thức, nếu có, phải là một ước của hệ số tự do.

Ví dụ 8. Phân tích đa thức f(x) = x3 x2 4 thành nhân tử.

Lời giải

Lần lượt kiểm tra với x = ± 1, ± 2, 4, ta thấy f(–2) = (–2)3 (–2)2 4 = 0. Đa thức f(x) có một nghiệm x = –2, do đó nó chứa một nhân tử là x 2. Từ đó, ta tách như sau

Cách 1 : f(x) = x3 2×2 – x2 4 = (x3 2×2) – (x2 – 4) = x2(x 2) – (x – 2)(x 2)

= (x 2)(x2 – x 2).

Cách 2 : f(x) = (x3 Cool (x2 – 4) = (x 2)(x2 – 2x 4) (x – 2)(x 2)

= (x 2)(x2 – x 2).

Cách 3 : f(x) = (x3 4×2 4x) – (3×2 6x) (2x 4)

= x(x 2)2 – 3x(x 2) 2(x 2) = (x 2)(x2 – x 2).

Cách 4 : f(x) = (x3 – x2 2x) (2×2 – 2x 4) = x(x2 – x 2) 2(x2 – x 2)

= (x 2)(x2 – x 2).

Từ định lí trên, ta có các hệ quả sau :

Hệ quả 1. Nếu f(x) có tổng các hệ số bằng 0 thì f(x) có một nghiệm là x = 1. Từ đó f(x) có một nhân tử là x – 1.

Chẳng hạn, đa thức x3 – 5×2 8x – 4 có 1 (–5) 8 (–4) = 0 nên x = 1 là một nghiệm của đa thức. Đa thức có một nhân tử là x – 1. Ta phân tích như sau :

Xem thêm : 30 kiểu tóc ngắn hàn quốc cho bạn gái cưng mê mẩn, 33 kiểu tóc hàn quốc đẹp nhất 2020 cho nữ

f(x) = (x3 – x2) – (4×2 – 4x) (4x – 4) = x2(x – 1) – 4x(x – 1) 4(x – 1)

= (x – 1)( x – 2)2

Hệ quả 2. Nếu f(x) có tổng các hệ số của các luỹ thừa bậc chẵn bằng tổng các hệ số của các luỹ thừa bậc lẻ thì f(x) có một nghiệm x = –1. Từ đó f(x) có một nhân tử là x 1.

Chẳng hạn, đa thức x3 – 5×2 3x 9 có 1 3 = –5 9 nên x = –1 là một nghiệm của đa thức. Đa thức có một nhân tử là x 1. Ta phân tích như sau :

f(x) = (x3 x2) – (6×2 6x) (9x 9) = x2(x 1) – 6x(x 1) 9(x 1)

= (x 1)( x – 3)2

Hệ quả 3. Nếu f(x) có nghiệm nguyên x = a và f(1) và f(–1) khác 0 thì và đều là số nguyên.

Ví dụ 9. Phân tích đa thức f(x) = 4×3 – 13×2 9x – 18 thành nhân tử.

Hướng dẫn

Các ước của 18 là ± 1, ± 2, ± 3, ± 6, ± 9, ± 18.

f(1) = –18, f(–1) = –44, nên ± 1 không phải là nghiệm của f(x).

Dễ thấy không là số nguyên nên –3, ± 6, ± 9, ± 18 không là nghiệm của f(x). Chỉ còn –2 và 3. Kiểm tra ta thấy 3 là nghiệm của f(x). Do đó, ta tách các hạng tử như sau :

= (x – 3)(4×2 – x 6)

Hệ quả 4. Nếu (là các số nguyên) có nghiệm hữu tỉ , trong đó p, q Z và (p , q)=1, thì p là ước a0, q là ước dương của an .

Ví dụ 10. Phân tích đa thức f(x) = 3×3 – 7×2 17x – 5 thành nhân tử.

Hướng dẫn

Các ước của –5 là ± 1, ± 5. Thử trực tiếp ta thấy các số này không là nghiệm của f(x). Như vậy f(x) không có nghiệm nghuyên. Xét các số , ta thấy là nghiệm của đa thức, do đó đa thức có một nhân tử là 3x – 1. Ta phân tích như sau :

f(x) = (3×3 – x2) – (6×2 – 2x) (15x – 5) = (3x – 1)(x2 – 2x 5).

IV. PHƯƠNG PHÁP THÊM VÀ BỚT CÙNG MỘT HẠNG TỬ

1. Thêm và bớt cùng một hạng tử làm xuất hiện hiệu hai bình phương

Ví dụ 12. Phân tích đa thức x4 x2 1 thành nhân tử

Lời giải

Cách 1 : x4 x2 1 = (x4 2×2 1) – x2 = (x2 1)2 – x2 = (x2 – x 1)(x2 x 1).

Cách 2 : x4 x2 1 = (x4 – x3 x2) (x3 1) = x2(x2 – x 1) (x 1)(x2 – x 1)

= (x2 – x 1)(x2 x 1).

Cách 3 : x4 x2 1 = (x4 x3 x2) – (x3 – 1) = x2(x2 x 1) (x – 1)(x2 x 1)

= (x2 – x 1)(x2 x 1).

Ví dụ 13. Phân tích đa thức x4 16 thành nhân tử

Lời giải

Cách 1 : x4 4 = (x4 4×2 4) – 4×2 = (x2 2)2 – (2x)2 = (x2 – 2x 2)(x2 2x 2)

Cách 2 : x4 4 = (x4 2×3 2×2) – (2×3 4×2 4x) (2×2 4x 4)

= (x2 – 2x 2)(x2 2x 2)

2. Thêm và bớt cùng một hạng tử làm xuất hiện nhân tử chung

Ví dụ 14. Phân tích đa thức x5 x – 1 thành nhân tử

Lời giải

Cách 1.

x5 x – 1 = x5 – x4 x3 x4 – x3 x2 – x2 x – 1

= x3(x2 – x 1) – x2(x2 – x 1) – (x2 – x 1)

= (x2 – x 1)(x3 – x2 – 1).

Cách 2. Thêm và bớt x2 :

x5 x – 1 = x5 x2 – x2 x – 1 = x2(x3 1) – (x2 – x 1)

= (x2 – x 1)[x2(x 1) – 1] = (x2 – x 1)(x3 – x2 – 1).

Ví dụ 15. Phân tích đa thức x7 x 1 thành nhân tử

Lời giải

x7 x2 1 = x7 – x x2 x 1 = x(x6 – 1) (x2 x 1)

= x(x3 – 1)(x3 1) (x2 x 1)

= x(x3 1)(x – 1)(x2 x 1) ( x2 x 1)

= (x2 x 1)(x5 – x4 – x2 – x 1)

Lưu ý : Các đa thức dạng x3m 1 x3n 2 1 như x7 x2 1, x4 x5 1 đều chứa nhân tử là x2 x 1.

V. PHƯƠNG PHÁP ĐỔI BIẾN

Đặt ẩn phụ để đưa về dạng tam thức bậc hai rồi sử dụng các phương pháp cơ bản.

Ví dụ 16. Phân tích đa thức sau thành nhân tử :

x(x 4)(x 6)(x 10) 128

Lời giải

x(x 4)(x 6)(x 10) 128 = (x2 10x)(x2 10x 24) 128

Đặt x2 10x 12 = y, đa thức đã cho có dạng :

(y – 12)(y 12) 128 = y2 – 16 = (y 4)(y – 4) = (x2 10x 16)(x2 10x Cool

= (x 2)(x Cool (x2 10x Cool

Nhận xét: Nhờ phương pháp đổi biến ta đã đưa đa thức bậc 4 đối với x thành đa thức bậc 2 đối với y.

Ví dụ 17. Phân tích đa thức sau thành nhân tử :

A = x4 6×3 7×2 – 6x 1.

Lời giải

Cách 1. Giả sử x ≠ 0. Ta viết đa thức dưới dạng :

Đặt thì . Do đó :

A = x2(y2 2 6y 7) = x2(y 3)2 = (xy 3x)2

= = (x2 3x – 1)2.

Dạng phân tích này cũng đúng với x = 0.

Cách 2. A = x4 6×3 – 2×2 9×2 – 6x 1 = x4 (6×3 -2×2) (9×2 – 6x 1)

= x4 2×2(3x – 1) (3x – 1)2 = (x2 3x – 1)2.

VI. PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNH

Ví dụ 18. Phân tích đa thức sau thành nhân tử :

x4 – 6×3 12×2 – 14x – 3

Lời giải

Thử với x= ±1; ±3 không là nghiệm của đa thức, đa thức không có nghiệm nguyên cũng không có nghiệm hữu tỷ. Như vậy đa thức trên phân tích được thành nhân tử thì phải có dạng

(x2 ax b)(x2 cx d) = x4 (a c)x3 (ac b d)x2 (ad bc)x bd

= x4 – 6×3 12×2 – 14x 3.

Đồng nhất các hệ số ta được :

Xét bd= 3 với b, d Î Z, b Î {± 1, ± 3}. Với b = 3 thì d = 1, hệ điều kiện trên trở thành

2c = -14 – (-6) = -8. Do đó c = -4, a = -2.

Vậy x4 – 6×3 12×2 – 14x 3 = (x2 – 2x 3)(x2 – 4x 1).

VII. PHƯƠNG PHÁP XÉT GIÁ TRỊ RIÊNG

Trong phương pháp này, trước hết ta xác định dạng các nhân tử chứa biến của đa thức, rồi gán cho các biến các giá trị cụ thể để xác định các nhân tử còn lại.

Ví dụ 19. Phân tích đa thức sau thành nhân tử :

P = x2(y – z) y2(z – x) z(x – y).

Lời giải

Thay x bởi y thì P = y2(y – z) y2( z – y) = 0. Như vậy P chứa thừa số (x – y).

Ta thấy nếu thay x bởi y, thay y bởi z, thay z bởi x thì p không đổi (đa thức P có thể hoán vị vòng quanh). Do đó nếu P đã chứa thừa số (x – y) thì cũng chứa thừa số (y – z), (z – x). Vậy P có dạng k(x – y)(y – z)(z – x).

Ta thấy k phải là hằng số vì P có bậc 3 đối với tập hợp các biến x, y, z, còn tích (x – y)(y – z)(z – x) cũng có bậc 3 đối với tập hợp các biến x, y, z.

Vì đẳng thức x2(y – z) y2(z – x) z2(x – y) = k(x – y)(y – z)(z – x) đúng với mọi x, y, z nên ta gán cho các biến x ,y, z các giá trị riêng, chẳng hạn x = 2, y = 1, z = 0 ta được:

4.1 1.(–2) 0 = k.1.1.(–2) suy ra k =1

Vậy P = –(x – y)(y – z)(z – x) = (x – y)(y – z)(x – z)

VIII. PHƯƠNG PHÁP ĐƯA VỀ MỘT SỐ ĐA THỨC ĐẶC BIỆT

1. Đưa về đa thức : a3 b3 c3 – 3abc

Ví dụ 20. Phân tích đa thức sau thành nhân tử :

a) a3 b3 c3 – 3abc.

b) (x – y)3 (y – z)3 (z – x)3.

Lời giải

a) a3 b3 c3 – 3abc = (a b)3 – 3a2b – 3ab2 c3 – 3abc

= [(a b)3 c3] – 3ab(a b c)

= (a b c)[(a b)2 – (a b)c c2] – 3ab(a b c)

= (a b c)(a2 b2 c2 – ab – bc -ca)

b) Đặt x – y = a, y – z = b, z – x = c thì a b c. Theo câu a) ta có :

a3 b3 c3 – 3abc = 0 Þ a3 b3 c3 = 3abc.

Vậy (x – y)3 (y – z)3 (z – x)3 = 3(x – y)(y – z)(z – x)

2. Đưa về đa thức : (a b c)3 – a3 – b3 – c3

Ví dụ 21. Phân tích đa thức sau thành nhân tử :

a) (a b c)3 – a3 – b3 – c3.

b) 8(x y z)3 – (x y)3 – (y z)3 – (z x)3.

Lời giải

a) (a b c)3 – a3 – b3 – c3 = [(a b) c]3 – a3 – b3 – c3

= (a b)3 c3 3c(a b)(a b c) – a3 – b3 – c3

= (a b)3 3c(a b)(a b c) – (a b)(a2 – ab b2)

= (a b)[(a b)2 3c(a b c) – (a2 – ab b2)]

= 3(a b)(ab bc ca c2) = 3(a b)[b(a c) c(a c)]

= 3(a b)(b c)(c a).

b) Đặt x y = a, y z = b, z x = c thì a b c = 2(a b c).

Đa thức đã cho có dạng : (a b c)3 – a3 – b3 – c3

Theo kết quả câu a) ta có :

(a b c)3 – a3 – b3 – c3 = 3(a b)(b c)(c a)

Hay 8(x y z)3 – (x y)3 – (y z)3 – (z x)3

= 3(x 2y z)(y 2z x)(z 2x y)

Các phương pháp phân tích đa thức thành nhân tửI. CÁC PHƯƠNG PHÁP CƠ BẢN1. Phương pháp đặt nhân tử chung– Tìm nhân tử chung là những đơn, đa thức có mặt trong tất cả các hạng tử.– Phân tích mỗi hạng tử thành tích của nhân tử chung và một nhân tử khác.– Viết nhân tử chung ra ngoài dấu ngoặc, viết các nhân tử còn lại của mỗi hạng tử vào trong dấu ngoặc (kể cả dấu của chúng).Ví dụ 1. Phân tích các đa thức sau thành nhân tử.28a2b2 – 21ab2 14a2b = 7ab(4ab – 3b 2a)2x(y – z) 5y(z –y ) = 2(y – z) – 5y(y – z) = (y – z)(2 – 5y)xm xm 3 = xm (x3 1) = xm( x 1)(x2 – x 1)2. Phương pháp dùng hằng đẳng thức- Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.- Cần chú ý đến việc vận dụng hằng đẳng thức.Ví dụ 2. Phân tích các đa thức sau thành nhân tử.9×2 – 4 = (3x)2 – 22 = ( 3x– 2)(3x 2)8 – 27a3b6 = 23 – (3ab2)3 = (2 – 3ab2)( 4 6ab2 9a2b4)25×4 – 10x2y y2 = (5×2 – y)23. Phương pháp nhóm nhiều hạng tử– Kết hợp các hạng tử thích hợp thành từng nhóm.– Áp dụng liên tiếp các phương pháp đặt nhân tử chung hoặc dùng hằng đẳng thức.Ví dụ 3. Phân tích các đa thức sau thành nhân tử2×3 – 3×2 2x – 3 = ( 2×3 2x) – (3×2 3) = 2x(x2 1) – 3( x2 1)= ( x2 1)( 2x – 3)x2 – 2xy y2 – 16 = (x – y)2 – 42 = ( x – y – 4)( x –y 4)4. Phối hợp nhiều phương pháp- Chọn các phương pháp theo thứ tự ưu tiên.- Đặt nhân tử chung.- Dùng hằng đẳng thức.- Nhóm nhiều hạng tử.Ví dụ 4. Phân tích các đa thức sau thành nhân tử3xy2 – 12xy 12x = 3x(y2 – 4y 4) = 3x(y – 2)23x3y – 6x2y – 3xy3 – 6axy2 – 3a2xy 3xy == 3xy(x2 – 2y – y2 – 2ay – a2 1)= 3xy[( x2 – 2x 1) – (y2 2ay a2)]= 3xy[(x – 1)2 – (y a)2]= 3xy[(x – 1) – (y a)][(x – 1) (y a)]= 3xy( x –1 – y – a)(x – 1 y a)II. PHƯƠNG PHÁP TÁCH MỘT HẠNG TỬ THÀNH NHIỀU HẠNG TỬ1. Đối với đa thức bậc hai (f(x) = ax2 bx c)a) Cách 1 (tách hạng tử bậc nhất bx):Bước 1: Tìm tích ac, rồi phân tích ac ra tích của hai thừa số nguyên bằng mọi cách.a.c = a1.c1 = a2.c2 = a3.c3 = … = ai.ci = …Bước 2: Chọn hai thừa số có tổng bằng b, chẳng hạn chọn tích a.c = ai.ci với b = ai ciBước 3: Tách bx = aix cix. Từ đó nhóm hai số hạng thích hợp để phân tích tiếp.Ví dụ 5. Phân tích đa thức f(x) = 3×2 8x 4 thành nhân tử.Hướng dẫn- Phân tích ac = 12 = 3.4 = (–3).(–4) = 2.6 = (–2).(–6) = 1.12 = (–1).(–12)- Tích của hai thừa số có tổng bằng b = 8 là tích a.c = 2.6 (a.c = ai.ci).- Tách 8x = 2x 6x (bx = aix cix)Lời giải3x2 8x 4 = 3×2 2x 6x 4 = (3×2 2x) (6x 4)= x(3x 2) 2(3x 2)= (x 2)(3x 2)b) Cách 2 (tách hạng tử bậc hai ax2)- Làm xuất hiện hiệu hai bình phương :f(x) = (4×2 8x 4) – x2 = (2x 2)2 – x2 = (2x 2 – x)(2x 2 x)= (x 2)(3x 2)- Tách thành 4 số hạng rồi nhóm :f(x) = 4×2 – x2 8x 4 = (4×2 8x) – ( x2 – 4) = 4x(x 2) – (x – 2)(x 2)= (x 2)(3x 2)f(x) = (12×2 8x) – (9×2 – 4) = … = (x 2)(3x 2)c) Cách 3 (tách hạng tử tự do c)- Tách thành 4 số hạng rồi nhóm thành hai nhóm:f(x) = 3×2 8x 16 – 12 = (3×2 – 12) (8x 16) = … = (x 2)(3x 2)d) Cách 4 (tách 2 số hạng, 3 số hạng)f(x) = (3×2 12x 12) – (4x= 3(x 2)2 – 4(x 2) = (x 2)(3x – 2)f(x) = (x2 4x 4) (2×2 4x) = … = (x 2)(3x 2)e) Cách 5 (nhẩm nghiệm): Xem phần III.Chú ý : Nếu f(x) = ax2 bx c có dạng A2 ± 2AB c thì ta tách như sau :f(x) = A2 ± 2AB B2 – B2 c = (A ± B)2 – (B2 – c)Ví dụ 6. Phân tích đa thức f(x) = 4×2 – 4x – 3 thành nhân tử.Hướng dẫnTa thấy 4×2 – 4x = (2x)2 – 2.2x. Từ đó ta cần thêm và bớt 12 = 1 để xuất hiện hằng đẳng thức.Lời giảif(x) = (4×2 – 4x 1) – 4 = (2x – 1)2 – 22 = (2x – 3)(2x 1)Ví dụ 7. Phân tích đa thức f(x) = 9×2 12x – 5 thành nhân tử.Lời giảiCách 1 : f(x) = 9×2 – 3x 15x – 5 = (9×2 – 3x) (15x – 5) = 3x(3x –1) 5(3x – 1)= (3x – 1)(3x 5)Cách 2 : f(x) = (9×2 12x 4) – 9 = (3x 2)2 – 32 = (3x – 1)(3x 5)2. Đối với đa thức bậc từ 3 trở lên (Xem mục III. Phương pháp nhẩm nghiệm)3. Đối với đa thức nhiều biếnVí dụ 11. Phân tích các đa thức sau thành nhân tửa) 2×2 – 5xy 2y2 ;b) x2(y – z) y2(z – x) z2(x – y).Hướng dẫna) Phân tích đa thức này tương tự như phân tích đa thức f(x) = ax2 bx c.Ta tách hạng tử thứ 2 :2×2 – 5xy 2y2 = (2×2 – 4xy) – (xy – 2y2) = 2x(x – 2y) – y(x – 2y)= (x – 2y)(2x – y)a) Nhận xét z – x = -(y – z) – (x – y). Vì vậy ta tách hạng tử thứ hai của đa thức :x2(y – z) y2(z – x) z2(x – y) = x2(y – z) – y2(y – z) – y2(x – y) z2(x – y) == (y – z)(x2 – y2) – (x – y)(y2 – z2) = (y – z)(x – y)(x y) – (x – y)(y – z)(y z)= (x – y)(y – z)(x – z)Chú ý :1) Ở câu b) ta có thể tách y – z = – (x – y) – (z – x) (hoặc z – x= – (y – z) – (x – y))2) Đa thức ở câu b) là một trong những đa thức có dạng đa thức đặc biệt. Khi ta thay x = y (y = z hoặc z = x) vào đa thức thì giá trị của đa thức bằng 0. Vì vậy, ngoài cách phân tích bằng cách tách như trên, ta còn cách phân tích bằng cách xét giá trị riêng (Xem phần VII).III. PHƯƠNG PHÁP NHẨM NGHIỆMTrước hết, ta chú ý đến một định lí quan trọng sau :Định lí : Nếu f(x) có nghiệm x = a thì f(a) = 0. Khi đó, f(x) có một nhân tử là x – a và f(x) có thể viết dưới dạng f(x) = (x – a).q(x)Lúc đó tách các số hạng của f(x) thành các nhóm, mỗi nhóm đều chứa nhân tử là x – a. Cũng cần lưu ý rằng, nghiệm nguyên của đa thức, nếu có, phải là một ước của hệ số tự do.Ví dụ 8. Phân tích đa thức f(x) = x3 x2 4 thành nhân tử.Lời giảiLần lượt kiểm tra với x = ± 1, ± 2, 4, ta thấy f(–2) = (–2)3 (–2)2 4 = 0. Đa thức f(x) có một nghiệm x = –2, do đó nó chứa một nhân tử là x 2. Từ đó, ta tách như sauCách 1 : f(x) = x3 2×2 – x2 4 = (x3 2×2) – (x2 – 4) = x2(x 2) – (x – 2)(x 2)= (x 2)(x2 – x 2).Cách 2 : f(x) = (x3(x2 – 4) = (x 2)(x2 – 2x 4) (x – 2)(x 2)= (x 2)(x2 – x 2).Cách 3 : f(x) = (x3 4×2 4x) – (3×2 6x) (2x 4)= x(x 2)2 – 3x(x 2) 2(x 2) = (x 2)(x2 – x 2).Cách 4 : f(x) = (x3 – x2 2x) (2×2 – 2x 4) = x(x2 – x 2) 2(x2 – x 2)= (x 2)(x2 – x 2).Từ định lí trên, ta có các hệ quả sau :Hệ quả 1. Nếu f(x) có tổng các hệ số bằng 0 thì f(x) có một nghiệm là x = 1. Từ đó f(x) có một nhân tử là x – 1.Chẳng hạn, đa thức x3 – 5×2 8x – 4 có 1 (–5) 8 (–4) = 0 nên x = 1 là một nghiệm của đa thức. Đa thức có một nhân tử là x – 1. Ta phân tích như sau :f(x) = (x3 – x2) – (4×2 – 4x) (4x – 4) = x2(x – 1) – 4x(x – 1) 4(x – 1)= (x – 1)( x – 2)2Hệ quả 2. Nếu f(x) có tổng các hệ số của các luỹ thừa bậc chẵn bằng tổng các hệ số của các luỹ thừa bậc lẻ thì f(x) có một nghiệm x = –1. Từ đó f(x) có một nhân tử là x 1.Chẳng hạn, đa thức x3 – 5×2 3x 9 có 1 3 = –5 9 nên x = –1 là một nghiệm của đa thức. Đa thức có một nhân tử là x 1. Ta phân tích như sau :f(x) = (x3 x2) – (6×2 6x) (9x 9) = x2(x 1) – 6x(x 1) 9(x 1)= (x 1)( x – 3)2Hệ quả 3. Nếu f(x) có nghiệm nguyên x = a và f(1) và f(–1) khác 0 thì và đều là số nguyên.Ví dụ 9. Phân tích đa thức f(x) = 4×3 – 13×2 9x – 18 thành nhân tử.Hướng dẫnCác ước của 18 là ± 1, ± 2, ± 3, ± 6, ± 9, ± 18.f(1) = –18, f(–1) = –44, nên ± 1 không phải là nghiệm của f(x).Dễ thấy không là số nguyên nên –3, ± 6, ± 9, ± 18 không là nghiệm của f(x). Chỉ còn –2 và 3. Kiểm tra ta thấy 3 là nghiệm của f(x). Do đó, ta tách các hạng tử như sau := (x – 3)(4×2 – x 6)Hệ quả 4. Nếu (là các số nguyên) có nghiệm hữu tỉ , trong đó p, q Z và (p , q)=1, thì p là ước a0, q là ước dương của an .Ví dụ 10. Phân tích đa thức f(x) = 3×3 – 7×2 17x – 5 thành nhân tử.Hướng dẫnCác ước của –5 là ± 1, ± 5. Thử trực tiếp ta thấy các số này không là nghiệm của f(x). Như vậy f(x) không có nghiệm nghuyên. Xét các số , ta thấy là nghiệm của đa thức, do đó đa thức có một nhân tử là 3x – 1. Ta phân tích như sau :f(x) = (3×3 – x2) – (6×2 – 2x) (15x – 5) = (3x – 1)(x2 – 2x 5).IV. PHƯƠNG PHÁP THÊM VÀ BỚT CÙNG MỘT HẠNG TỬ1. Thêm và bớt cùng một hạng tử làm xuất hiện hiệu hai bình phươngVí dụ 12. Phân tích đa thức x4 x2 1 thành nhân tửLời giảiCách 1 : x4 x2 1 = (x4 2×2 1) – x2 = (x2 1)2 – x2 = (x2 – x 1)(x2 x 1).Cách 2 : x4 x2 1 = (x4 – x3 x2) (x3 1) = x2(x2 – x 1) (x 1)(x2 – x 1)= (x2 – x 1)(x2 x 1).Cách 3 : x4 x2 1 = (x4 x3 x2) – (x3 – 1) = x2(x2 x 1) (x – 1)(x2 x 1)= (x2 – x 1)(x2 x 1).Ví dụ 13. Phân tích đa thức x4 16 thành nhân tửLời giảiCách 1 : x4 4 = (x4 4×2 4) – 4×2 = (x2 2)2 – (2x)2 = (x2 – 2x 2)(x2 2x 2)Cách 2 : x4 4 = (x4 2×3 2×2) – (2×3 4×2 4x) (2×2 4x 4)= (x2 – 2x 2)(x2 2x 2)2. Thêm và bớt cùng một hạng tử làm xuất hiện nhân tử chungVí dụ 14. Phân tích đa thức x5 x – 1 thành nhân tửLời giảiCách 1.×5 x – 1 = x5 – x4 x3 x4 – x3 x2 – x2 x – 1= x3(x2 – x 1) – x2(x2 – x 1) – (x2 – x 1)= (x2 – x 1)(x3 – x2 – 1).Cách 2. Thêm và bớt x2 :x5 x – 1 = x5 x2 – x2 x – 1 = x2(x3 1) – (x2 – x 1)= (x2 – x 1)[x2(x 1) – 1] = (x2 – x 1)(x3 – x2 – 1).Ví dụ 15. Phân tích đa thức x7 x 1 thành nhân tửLời giảix7 x2 1 = x7 – x x2 x 1 = x(x6 – 1) (x2 x 1)= x(x3 – 1)(x3 1) (x2 x 1)= x(x3 1)(x – 1)(x2 x 1) ( x2 x 1)= (x2 x 1)(x5 – x4 – x2 – x 1)Lưu ý : Các đa thức dạng x3m 1 x3n 2 1 như x7 x2 1, x4 x5 1 đều chứa nhân tử là x2 x 1.V. PHƯƠNG PHÁP ĐỔI BIẾNĐặt ẩn phụ để đưa về dạng tam thức bậc hai rồi sử dụng các phương pháp cơ bản.Ví dụ 16. Phân tích đa thức sau thành nhân tử :x(x 4)(x 6)(x 10) 128Lời giảix(x 4)(x 6)(x 10) 128 = (x2 10x)(x2 10x 24) 128Đặt x2 10x 12 = y, đa thức đã cho có dạng :(y – 12)(y 12) 128 = y2 – 16 = (y 4)(y – 4) = (x2 10x 16)(x2 10x= (x 2)(x(x2 10xNhận xét: Nhờ phương pháp đổi biến ta đã đưa đa thức bậc 4 đối với x thành đa thức bậc 2 đối với y.Ví dụ 17. Phân tích đa thức sau thành nhân tử :A = x4 6×3 7×2 – 6x 1.Lời giảiCách 1. Giả sử x ≠ 0. Ta viết đa thức dưới dạng :Đặt thì . Do đó :A = x2(y2 2 6y 7) = x2(y 3)2 = (xy 3x)2= = (x2 3x – 1)2.Dạng phân tích này cũng đúng với x = 0.Cách 2. A = x4 6×3 – 2×2 9×2 – 6x 1 = x4 (6×3 -2×2) (9×2 – 6x 1)= x4 2×2(3x – 1) (3x – 1)2 = (x2 3x – 1)2.VI. PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNHVí dụ 18. Phân tích đa thức sau thành nhân tử :x4 – 6×3 12×2 – 14x – 3Lời giảiThử với x= ±1; ±3 không là nghiệm của đa thức, đa thức không có nghiệm nguyên cũng không có nghiệm hữu tỷ. Như vậy đa thức trên phân tích được thành nhân tử thì phải có dạng(x2 ax b)(x2 cx d) = x4 (a c)x3 (ac b d)x2 (ad bc)x bd= x4 – 6×3 12×2 – 14x 3.Đồng nhất các hệ số ta được :Xét bd= 3 với b, d Î Z, b Î {± 1, ± 3}. Với b = 3 thì d = 1, hệ điều kiện trên trở thành2c = -14 – (-6) = -8. Do đó c = -4, a = -2.Vậy x4 – 6×3 12×2 – 14x 3 = (x2 – 2x 3)(x2 – 4x 1).VII. PHƯƠNG PHÁP XÉT GIÁ TRỊ RIÊNGTrong phương pháp này, trước hết ta xác định dạng các nhân tử chứa biến của đa thức, rồi gán cho các biến các giá trị cụ thể để xác định các nhân tử còn lại.Ví dụ 19. Phân tích đa thức sau thành nhân tử ? = x2(y – z) y2(z – x) z(x – y).Lời giảiThay x bởi y thì P = y2(y – z) y2( z – y) = 0. Như vậy P chứa thừa số (x – y).Ta thấy nếu thay x bởi y, thay y bởi z, thay z bởi x thì p không đổi (đa thức P có thể hoán vị vòng quanh). Do đó nếu P đã chứa thừa số (x – y) thì cũng chứa thừa số (y – z), (z – x). Vậy P có dạng k(x – y)(y – z)(z – x).Ta thấy k phải là hằng số vì P có bậc 3 đối với tập hợp các biến x, y, z, còn tích (x – y)(y – z)(z – x) cũng có bậc 3 đối với tập hợp các biến x, y, z.Vì đẳng thức x2(y – z) y2(z – x) z2(x – y) = k(x – y)(y – z)(z – x) đúng với mọi x, y, z nên ta gán cho các biến x ,y, z các giá trị riêng, chẳng hạn x = 2, y = 1, z = 0 ta được:4.1 1.(–2) 0 = k.1.1.(–2) suy ra k =1Vậy P = –(x – y)(y – z)(z – x) = (x – y)(y – z)(x – z)VIII. PHƯƠNG PHÁP ĐƯA VỀ MỘT SỐ ĐA THỨC ĐẶC BIỆT1. Đưa về đa thức : a3 b3 c3 – 3abcVí dụ 20. Phân tích đa thức sau thành nhân tử :a) a3 b3 c3 – 3abc.b) (x – y)3 (y – z)3 (z – x)3.Lời giảia) a3 b3 c3 – 3abc = (a b)3 – 3a2b – 3ab2 c3 – 3abc= [(a b)3 c3] – 3ab(a b c)= (a b c)[(a b)2 – (a b)c c2] – 3ab(a b c)= (a b c)(a2 b2 c2 – ab – bc -ca)b) Đặt x – y = a, y – z = b, z – x = c thì a b c. Theo câu a) ta có :a3 b3 c3 – 3abc = 0 Þ a3 b3 c3 = 3abc.Vậy (x – y)3 (y – z)3 (z – x)3 = 3(x – y)(y – z)(z – x)2. Đưa về đa thức : (a b c)3 – a3 – b3 – c3Ví dụ 21. Phân tích đa thức sau thành nhân tử :a) (a b c)3 – a3 – b3 – c3.b) 8(x y z)3 – (x y)3 – (y z)3 – (z x)3.Lời giảia) (a b c)3 – a3 – b3 – c3 = [(a b) c]3 – a3 – b3 – c3= (a b)3 c3 3c(a b)(a b c) – a3 – b3 – c3= (a b)3 3c(a b)(a b c) – (a b)(a2 – ab b2)= (a b)[(a b)2 3c(a b c) – (a2 – ab b2)]= 3(a b)(ab bc ca c2) = 3(a b)[b(a c) c(a c)]= 3(a b)(b c)(c a).b) Đặt x y = a, y z = b, z x = c thì a b c = 2(a b c).Đa thức đã cho có dạng : (a b c)3 – a3 – b3 – c3Theo kết quả câu a) ta có :(a b c)3 – a3 – b3 – c3 = 3(a b)(b c)(c a)Hay 8(x y z)3 – (x y)3 – (y z)3 – (z x)3= 3(x 2y z)(y 2z x)(z 2x y)

Xem thêm : Có nên học tiếng anh khi ngủ? cách học nghe tiếng anh khi ngủ thế nào?

Về Đầu Trang Go down