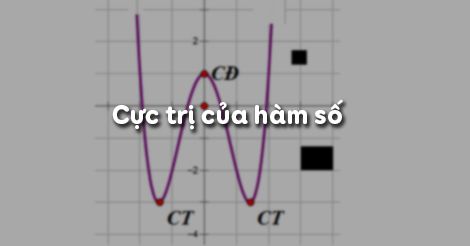
Toán 12 bài 2: cực trị của hàm số

Bạn đang xem: toán 12 bài 2: cực trị của hàm số Tại Pkmacbook.com

Mục lục hiện

Tóm tắt lý thuyết

Cho hàm số \(y=f(x)\) liên tục trên khoảng (a;b) và điểm \(x_0\in(a;b)\):

Hàm số \(f(x)\) đạt cực đại tại \(x_0\) nếu \(f(x_0)>f(x) \ \forall x\in (x_0-h,x_0+h) \setminus \left \{ x_0 \right \},h>0\)
Hàm số \(f(x)\) đạt cực tiểu tại x0 nếu \(f(x_0)0\).

a) Điều kiện cần để hàm số có cực trị

\(f(x)\) đạt cực trị tại \(x_0\), có đạo hàm tại \(x_0\) thì \(f'(x_0)=0\).

b) Điều kiện đủ để hàm số có điểm cực đại và cực tiểu

Điều kiện thứ nhất: Cho hàm số \(y=f(x)\) liên tục trên khoảng \(K = ({x_0} – h;{x_0} + h)\,(h > 0)\) và có đạo hàm trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\):
- Nếu thì x0 là điểm cực tiểu của hàm số \(f(x)\).
- Nếu thì x0 là điểm cực đại của hàm số \(f(x)\).
Cách phát biểu khác dễ hiểu hơn: Đi từ trái sang phải
- Nếu \(f(x)\) đổi dấu từ – sang + khi qua \(x_0\) thì \(x_0\) là điểm cực tiểu.
- Nếu \(f(x)\) đổi dấu từ + sang – khi qua \(x_0\) thì \(x_0\) là điểm cực đại.
Điều kiện thứ hai:

Cho hàm số \(y=f(x)\) có đạo hàm cấp hai trên khoảng

\(K = ({x_0} – h;{x_0} + h)\,(h > 0)\):
- Nếu
  
  \(f'(x_0)=0\)
  
  , \(f”(x_0)
  
  \(x_0\)
  
  là điểm cực đại của hàm số \(f(x)\).
- Nếu
  
  \(f'(x_0)=0\)
  
  ,
  
  \(f”(x_0)>0\)
  
  thì
  
  \(x_0\)
  
  là điểm cực tiểu của hàm số \(f(x)\).